XtalOpt - About XtalOpt

XtalOpt is a free and truly open source multi-objective evolutionary algorithm designed for a priori prediction of functional materials with a fixed or variable composition.

Detailed user guide for the latest version of XtalOpt and the description of the implemented methodology:

User Guide Methodology

Quick overview of the XtalOpt code features:

Graphical User Interface Multi-Objective Search Evolutionary Operations

Graphical User Interface

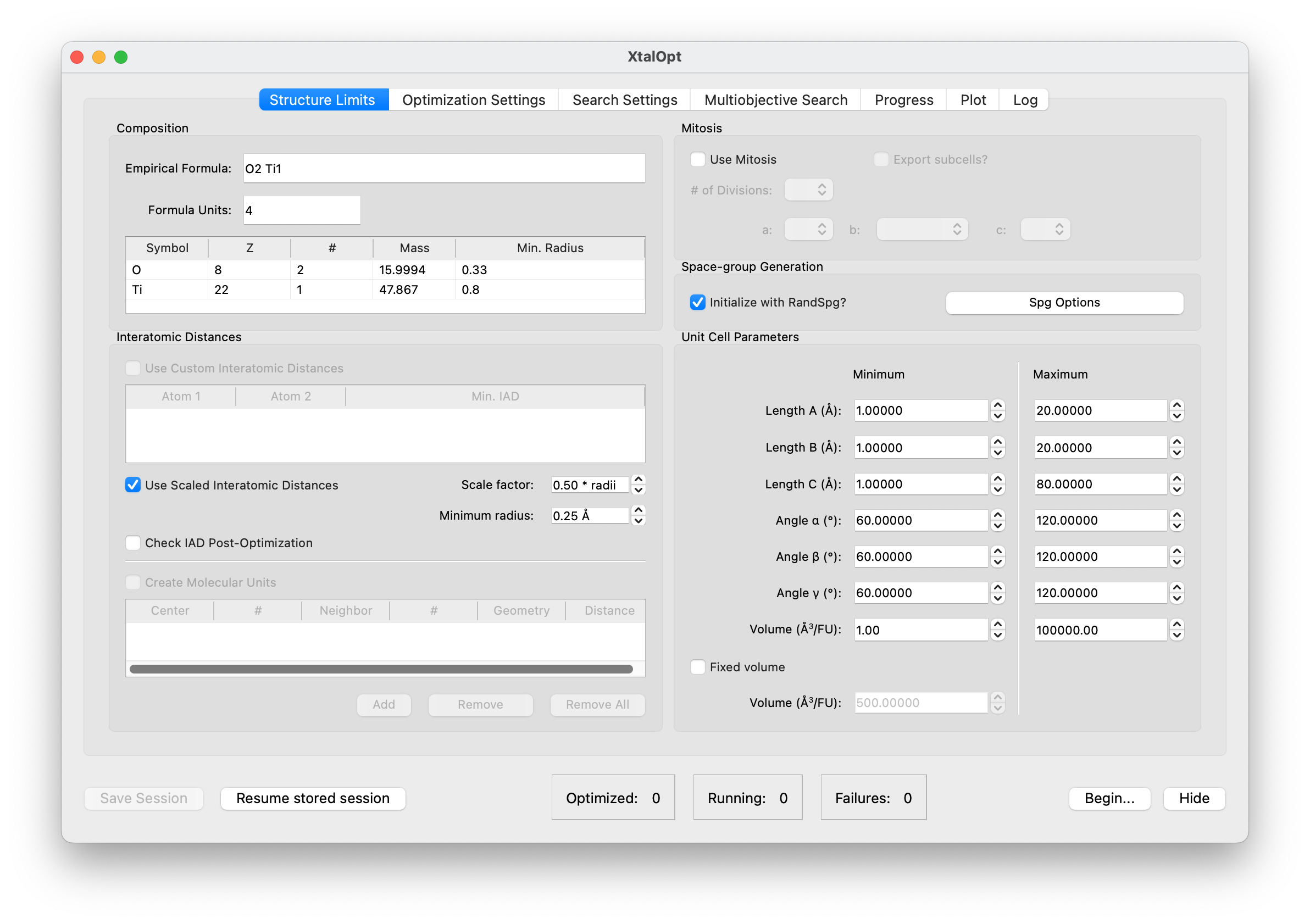
Structure Limits

The "Structure Limits" tab

This tab is where the user defines the reference chemical system, search type, and parameters of the each cell generated during the search.
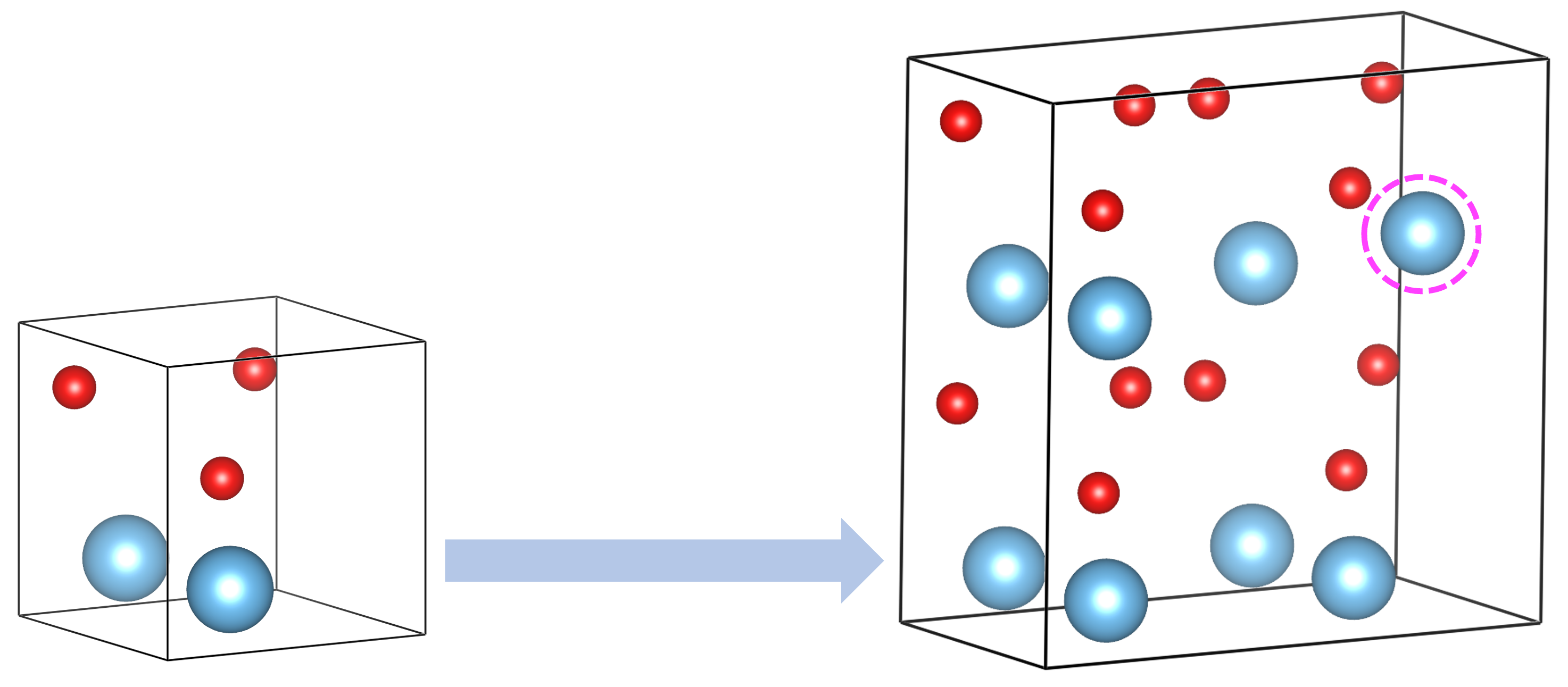
The user can specify a list of chemical formulas for the first generation of structures (e.g., Ti1O2, Ti2O3).
Also, the search type can be chosen from fixed, multi, or variable composition.
A range can be set for the length of each cell vector (a, b, and c) and the corresponding angles (α, β, and γ).
The combination of the cell vector lengths determines the cell volume, but the user can set a limited range for the volume per atom, limits for elemental volumes, or factors of estimated covalent volume.
Limiting the interatomic distances ensures the program is not generating nonsensical structures.
RandSpg or molecular unit builder can be used to generate the first population of structures.

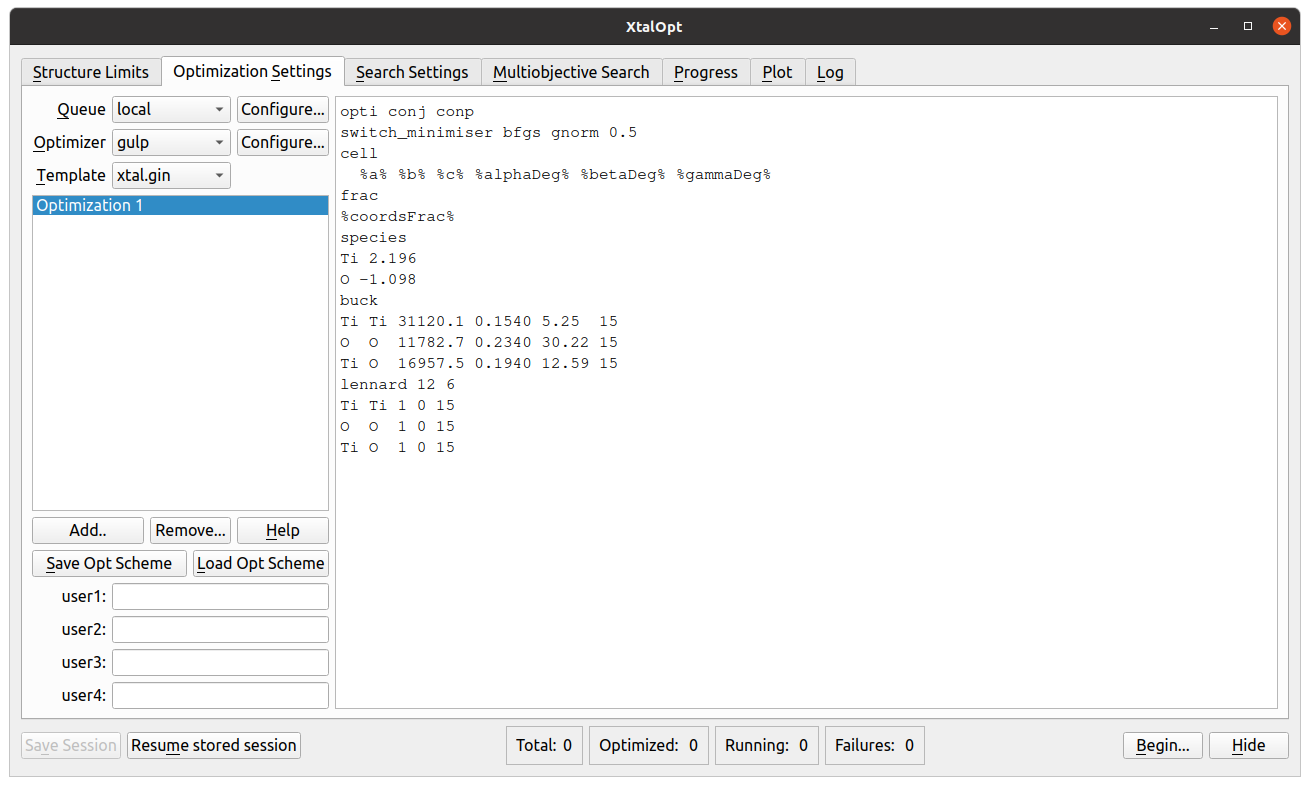
Optimization Settings

Choose from several queueing systems and optimizer combinations.
Queue systems supported include: SLURM, PBS, LSF, etc.
Optimizers include: VASP, GULP, CASTEP, etc.

The "Optimization Settings" tab

Search Settings

The "Search Settings" tab

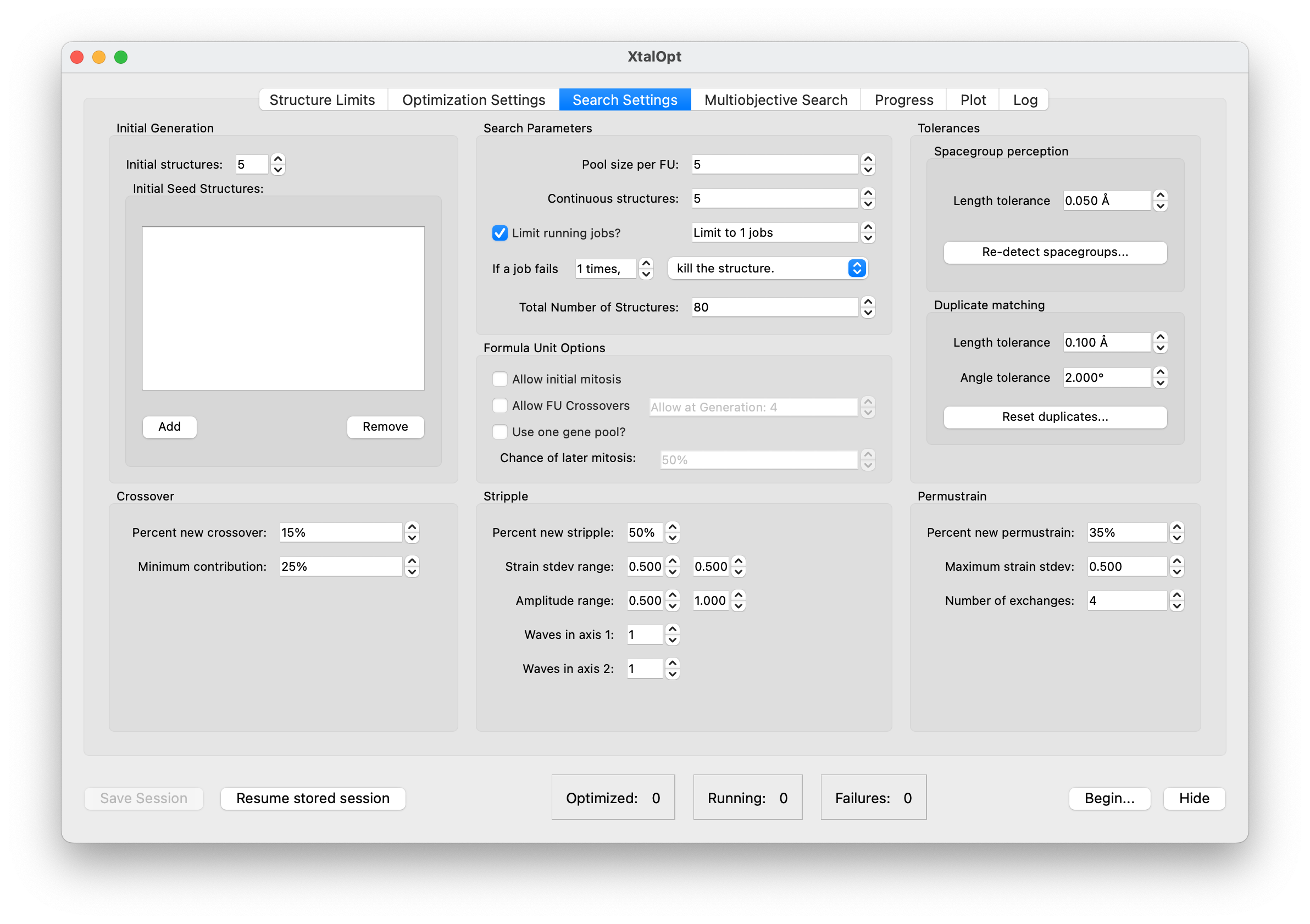
"Search Settings" is where the user can alter how the search will proceed.
The number of randomly generated initial structures and number of concurrently running structures are controlled in this tab.
The termination criteria of final number of structures can be set here, as well.
Users can adjust the relative chance of occurrence of each operator type.
Furthermore, the individual parameters of each operator can be fine tuned (number of exchanges in a "permustrain" or minimum contribution from a parent during a "crossover").
Similarity check schemes and their parameters are also found here.

Multiobjective Search

To utilize the multi-objective search functionality of XtalOpt, the user can add desired "objectives", i.e., any property that can be calculated for a structure, for simultaneous optimization with total enthalpy.
The "Multiobjective Search" tab allows the user to specify for each objective:
- the objective type,
- corresponding weight,
- path to the (potentially) external code or script that calculates that objective,
- the output file name of the external code for reading the corresponding calculated value.
In this tab, the user can also choose the global optimization type from "Basic" or "Pareto", and fine-tune relevant parameters.

The "Multiobjective Search" tab

Progress

As XtalOpt performs the search, the progress table continuously updates, providing information about each structure.
In the figure we see individuals in various stages of completion:

One structure XtalOpt displays is optimized (in blue), another structure has been automatically marked as a "similarity" (dark green) and removed from the breeding pool, yet another structure is currently undergoing a local optimization (light green), while another structure is waiting to be optimized. For a multi-objective run, while the objectives are being calculated, the structure is marked as calculating objectives (yellow). If these objective calculations fail, then the structure will be marked as objective fail (gray).

Other useful information is displayed about each structure, such as the time spent in optimization, the optimized enthalpy per atom, calculated distance above hull and Pareto front (rank), the volume per atom, spacegroup, and each structure's ancestry (i.e. parent(s) and parameters for the evolutionary operator that generated it).
A status bar on the bottom of the window shows the total number of generated structures, number of structures that are optimized, running, and failing at any given time.
This information is updated regardless of which tab is currently being viewed.
An additional feature of the progress table is the ability to immediately visualize any of the individuals in the Avogadro main window – simply clicking on a row in this table will display the three-dimensional structure in Avogadro, where it can be visualized, modified, or exported.
If the user would like to add a bit of “intelligent design” to the evolutionary process, a structure can be modified and then resubmitted using a context (right-click) menu from the progress table.
The context menu provides tools to (un)kill a structure, resubmit for local optimization at an arbitrary optimization step, or replace a problematic structure with a new, random individual.

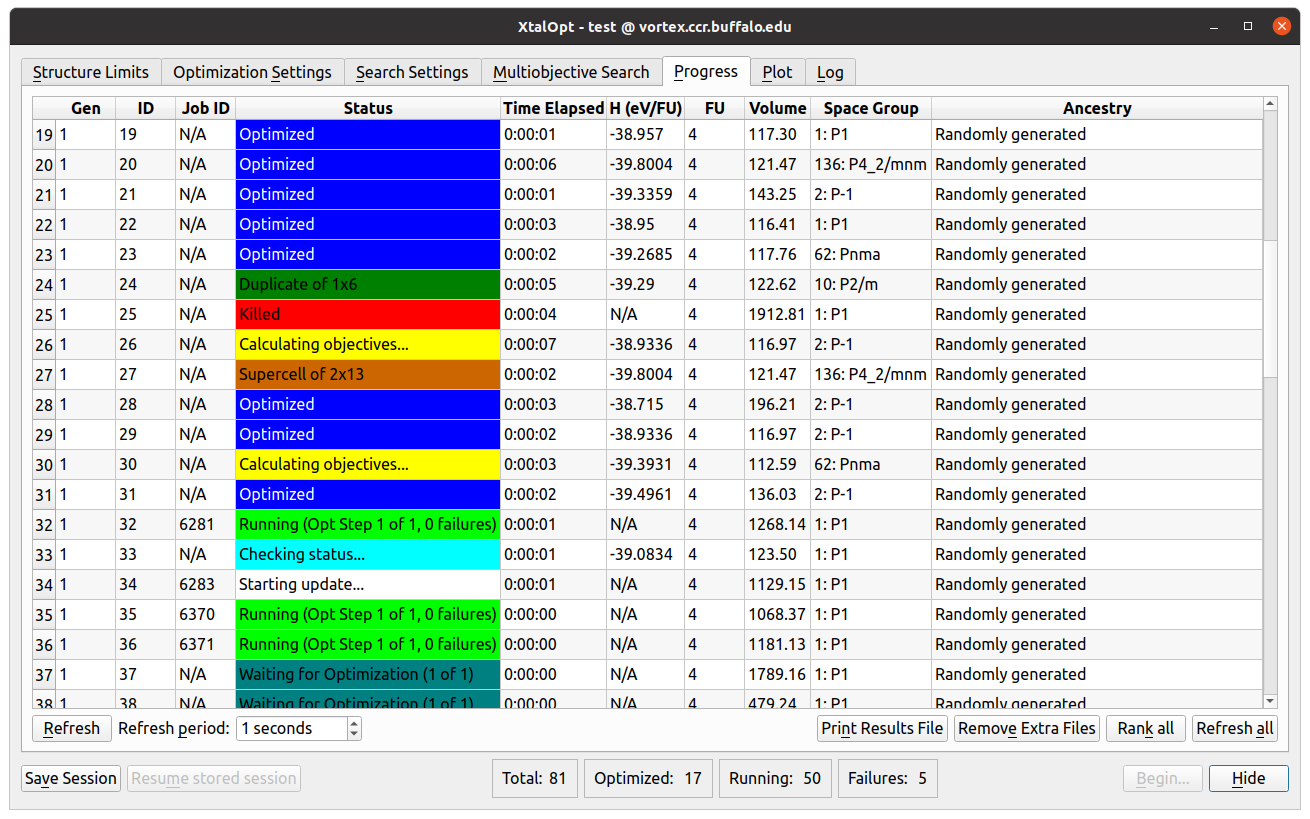
The "Progress" tab

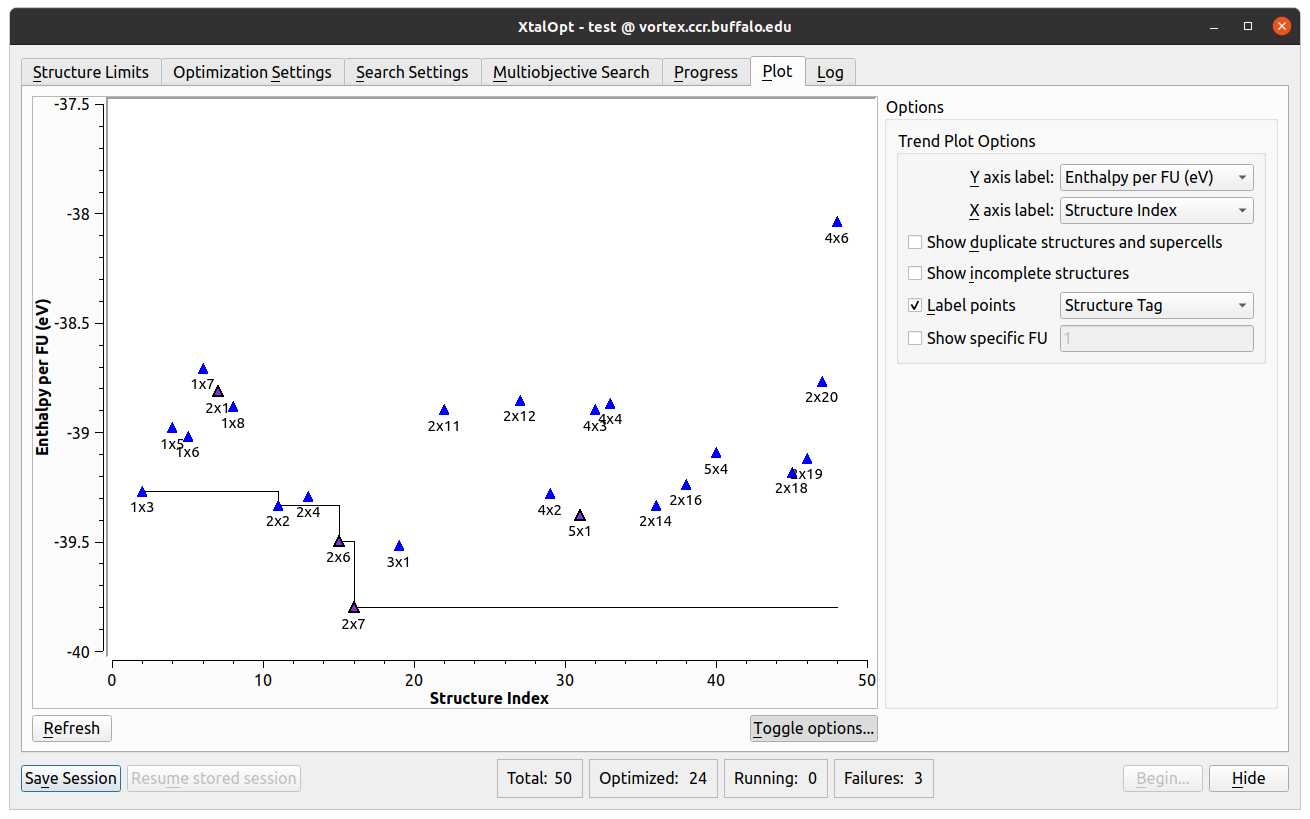
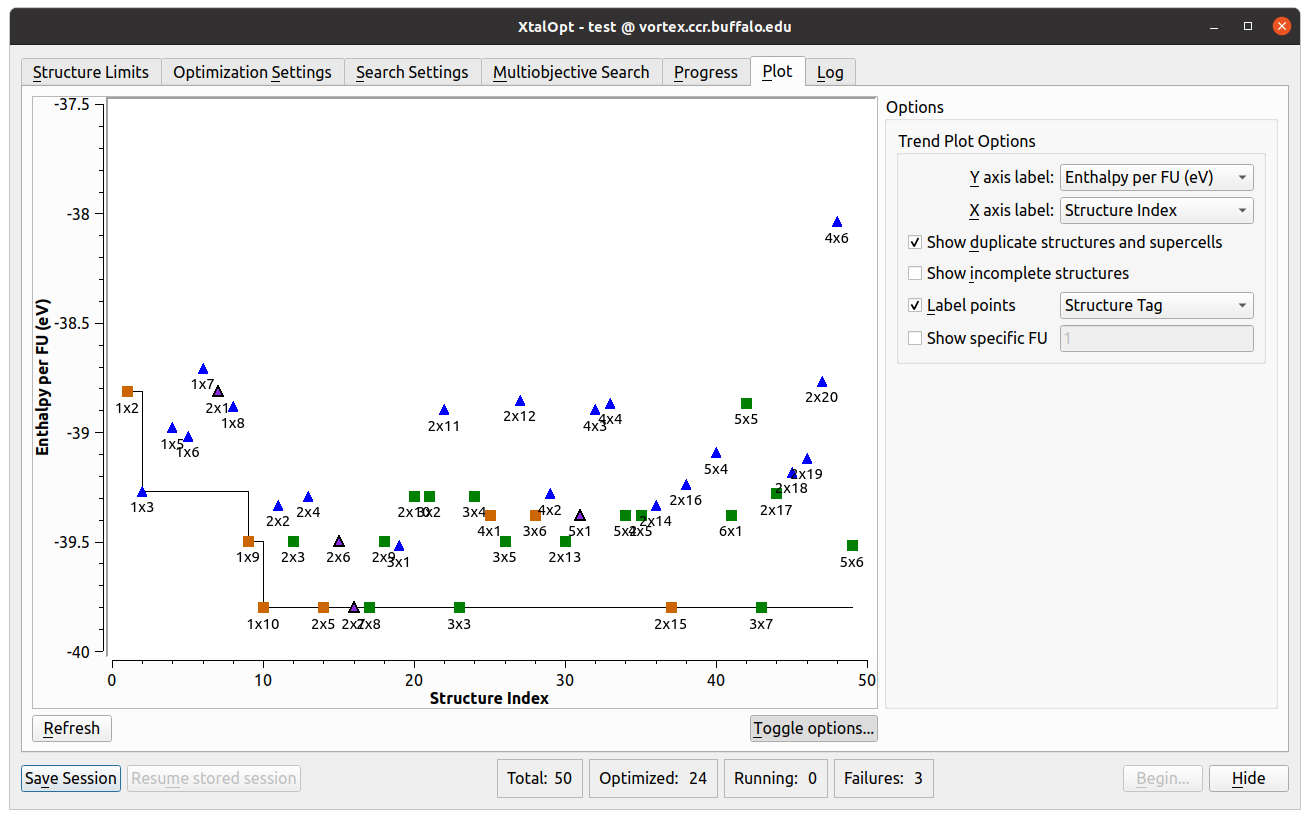
Plot

Another visualization and analysis tool available during the search is the interactive plot.
Allows investigation of various trends in the search by plotting a point for each individual.
Each point can be plotted based upon distance above hull, Pareto front, structure index, generation number, enthalpy, energy, PV enthalpy term, lattice parameters, cell volume, or objectives (in a multi-objective search) on either axis.
Further information is available by labeling the points with the individual’s structure tag, spacegroup number, Hermann-Mauguin spacegroup symbol, enthalpy, energy, PV term, volume, generation, or index number.
The plot is also interactive; zooming and panning are possible using simple mouse controls.
Clicking on a structure’s point in the plot will load it in the main Avogadro window, allowing all the same functionality as described above in the progress table section.

The "Plot" tab showing optimized (blue) structures

The "Plot" tab showing optimized structures (blue triangles) and those marked as similar (green squares).

Multi-Objective Search

User-specified objectives

The user can utilize an arbitrary number of objectives for multi-objective optimization.
Each objective is corresponding to a property of the system that can be calculated and represented with a single numerical value (enthalpy is a trivial one!).
After successful local optimization, XtalOpt provides the external code with structural information of the relaxed structure for calculating the desired property.
To introduce an objective, the user should specify the external code or script that calculates that property and the file name to which the corresponding numerical value is written.
Performing the multi-objective optimization, requires the user to further specify the optimization type and a weight for each objective to be used in calculating the generalized fitness function.

Basic generalized fitness function

XtalOpt uses a scalar generalized fitness function to assess the suitability of each structure in a multi-objective optimization.
For a set of objectives \(\{X\}\) and \(\{Y\}\) to be minimized and maximized, respectively, the generalized fitness function for \(s^\textrm{th}\) structure is calculated as:

\(f_s= \sum_i w^i_X \left( \frac{X^i_{max} - X^i_{s} }{X^i_{max}-X^i_{min}} \right) + \) \( \sum_j w^j_Y \left( \frac{Y^j_{s} - Y^j_{min}}{Y^j_{max}-Y^j_{min}} \right) \)

With the total objective weights' equal to 1.0, the fitness function will be a value between 0 and 1.
Choosing as many structures as the user-specified pool size according to the fitness value of candidate structures, an accumulative probability is being calculated. This probability will be used to chose a structure randomly for procreation by means of evolutionary operations.

Pareto optimization

Regardless of the number of objectives, XtalOpt can perform global optimization through Pareto optimization.
Within the NSGA-II algorithm, a non-dominated sorting is performed to obtain the ranks and (scaled) crowding distances of structures pool.
A new parent is then chosen through a "binary tournament selection".
Further, XtalOpt can -optionally- convert the rank-distance information to a scalar fitness measure and use that for parent selection.

Evolutionary Operations

crossover

permustrain

stripple

permutomic

permucomp

elementary mutators

secondary mutator

Elementary Mutator: Exchange

Exchange is the simplest mutator that exchanges two atoms of different types in a cell.

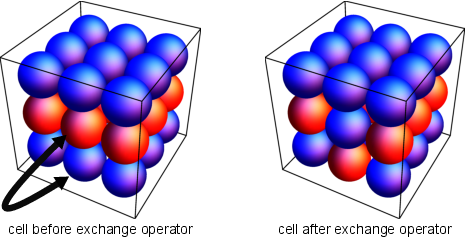
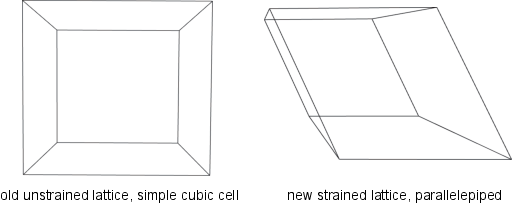
Elementary Mutator: Strain

The strain mutator allows XtalOpt to mutate the unit cell parameters, but not the fractional positions of the atoms. One can multiply the cell row vectors by the symmetric voight matrix, as shown below,

\( \vec{\textrm{v}}_{\textrm{new}} = \vec{\textrm{v}} \begin{bmatrix} 1+\varepsilon_{11} & \frac{\varepsilon_{12}}{2} & \frac{\varepsilon_{13}}{2} \\ \frac{\varepsilon_{12}}{2} & 1+\varepsilon_{22} & \frac{\varepsilon_{32}}{2} \\ \frac{\varepsilon_{13}}{2} & \frac{\varepsilon_{23}}{2} & 1+\varepsilon_{33} \end{bmatrix} \)

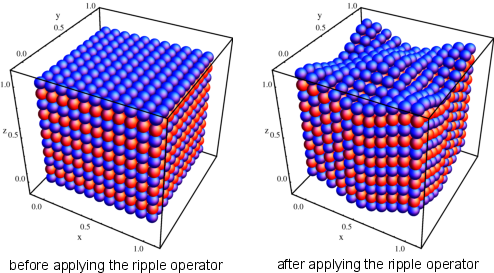
Elementary Mutator: Ripple

The ripple mutator acts as a periodic displacement of the atomic coordinates in a cell. A random axis is chosen (e.g., the \(z\) axis) and the atoms along this axis are shifted by an amount, \(\Delta z\), where the new coordinate along that axis will be \( z_\mathrm{new} = z + \Delta z \).
The displacement along the axis chosen is dependent on atomic placement in the orthogonal plane (\(x\) and \(y\) axes for this example) following the formula:

\( \Delta z = \rho\cos(2\pi\mu x+\theta_{x})\cos(2\pi\eta y+\theta_{y}), \) \(~~~~~\mu\in\mathbb{Z},~\eta\in\mathbb{Z} \)
In this equation:
- \(\rho\) is the maximum displacement of an atom along the axis.
- \(\mu\) and \(\eta\) determines the number of cosine waves in the orthogonal directions.
- \(\theta_{x}\) and \(\theta_{y}\) are randomly chosen values between \(0\) and \(2 \pi\) that specify the strength of the ripple in various areas of the cell.

Permustrain

The permustrain evolutionary operation combines two of the basic mutations, strain and exchange, to produce an offspring from a given parent structure.
The specifications of the strain operation can be set by the user, and the atoms to be exchanged are being selected randomly.

Stripple

Another evolutionary operation that mutates the parent structure, stripple, applies an strain followed by a ripple mutation to the selected parent cell.
The strain and ripple operations are performed according to the user-defined details for these steps.

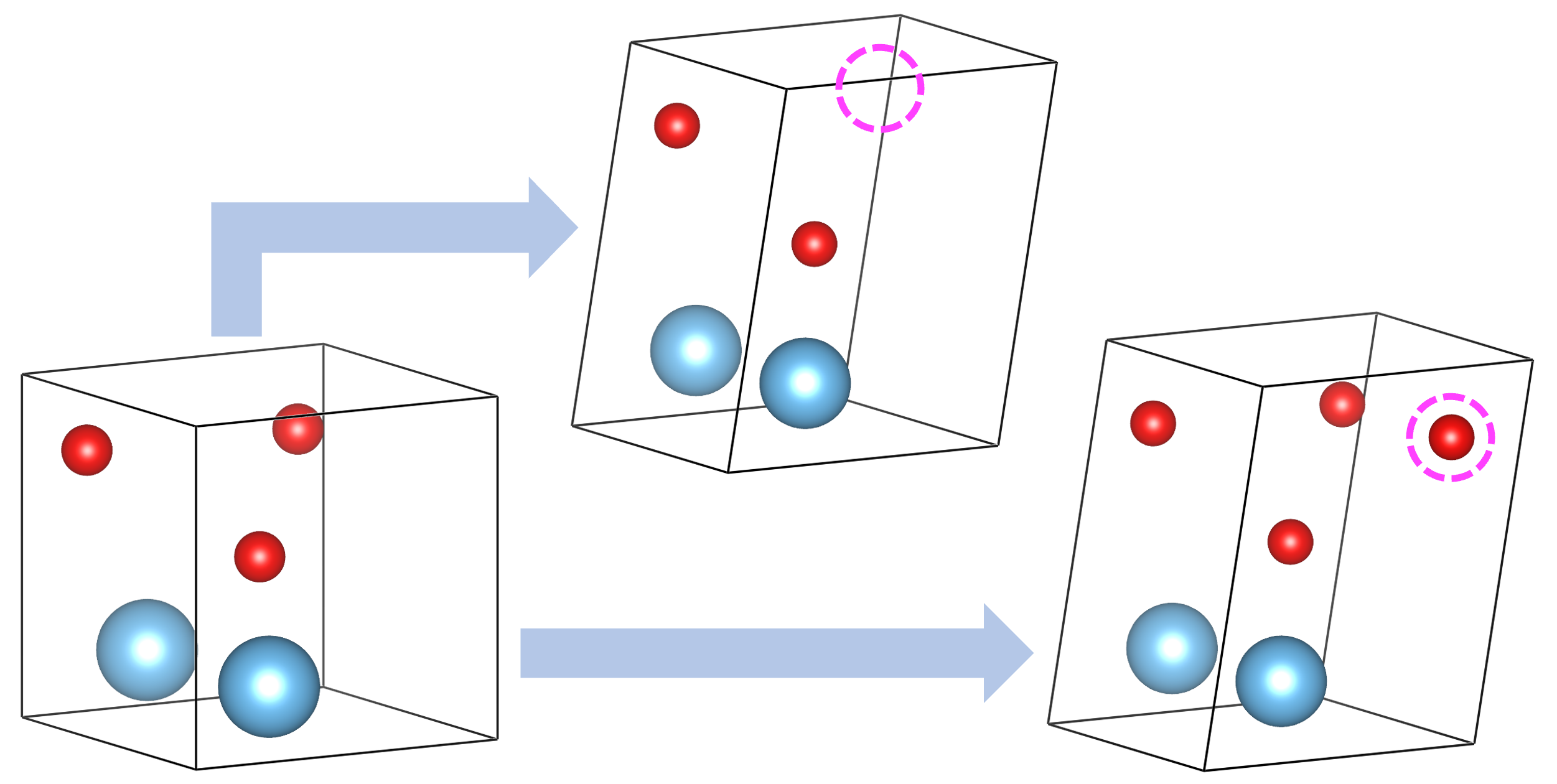
Permutomic

The permutomic operator performs an atomic mutation in the parent cell.
After applying a small strain to the parent cell, an atom is randomly added or removed, to produce the offspring.
This operation is designed for the variable-composition search.

Permucomp

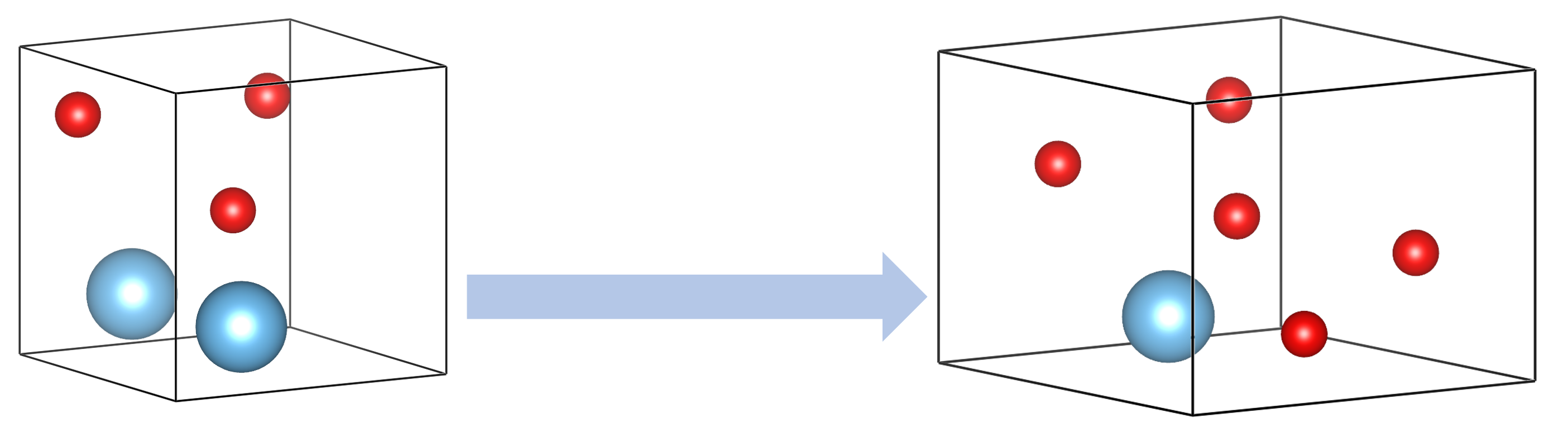
The permucomp, mutation of composition, is a genetic operation aimed at diversifying the structures pool by creating new random compositions.
This can be considered an "exotic permutomic"! While permutomic adds or removes one atom in the cell; permucomp creates a brand new composition.
Starting with slightly distorted parent cell through applying strain, a new random composition is produced and atoms are distributed in the cell accordingly.
As an operation that changes the composition, this is applicable only to variable-composition searches.

Crossover

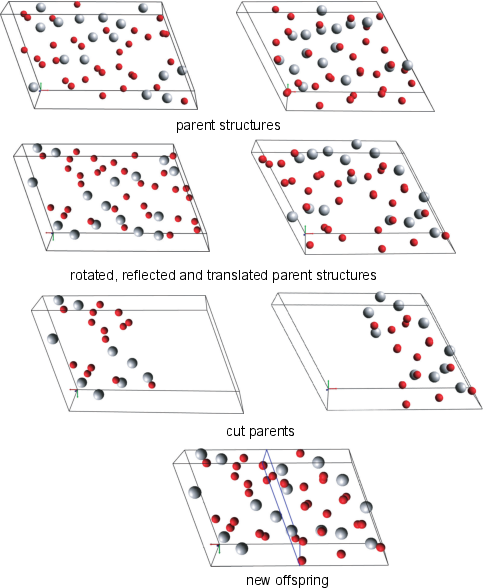
The crossover, or "cut and splice", operator is the equivalent of breeding in biology of breeding in which two parents are combined to form an offspring.
This is the only operator in XtalOpt that requires two parents to generate an offspring.
For XtalOpt's implementation, two parents are selected from the breeding pool.
The atoms in both parent structures are randomly reflected and rotated to avoid biasing one given orientation.
Each newly mutated parent is then "cut" to form the two halves of what will be the offspring structure.
Finally, the two halves are "spliced" together.
This occurs through first joining the atomic positions in fractional coordinates.
The cell dimensions are defined through random weighting of each of the parents' cell vectors.
The composition of offspring produced in crossover depends on the search type: for a fixed- or multi-composition search it is forced the have one of the parent structures' composition; while there is no such a restriction in a variable-composition search.

Secondary Mutator: Random Supercell Expansion

Random supercell expansion is a "pseudo"-genetic operation: it can be applied to the outcome of the above genetic operations, according to a user-specified probability.
Considering the total number of atoms in the starting cell and the maximum number of atoms specified by the user, three random expansion factors are determined and applied to obtain a supercell.
In the produced supercell, an atom is chosen and displaced randomly, subject to the minimum inter-atomic distance constrains.